What you see is not what you get

LLVM is the Low Level Virtual Machine. It’s a compiler backend- the deal is you compile your fancy high level language to a high level assembly and hand that off to LLVM. This high level assembly is the LLVM Intermediate Representation (IR). LLVM handles a bunch of optimizations and then compiles to machine code for whatever hardware platform you want. This is what VM’s do (think Java)- they give you portability across hardware & operating systems. LLVM’s assembly language is in Static Single Assignment form (SSA) because it was originally made with C and C++ in mind, but lots of other production languages, even functional ones like Haskell, Julia, Python (Numba), and Rust have compilers that target LLVM! You can roll your own compiler to target LLVM!

It’s really awesome because it means that if you want to write a language, LLVM modularizes your concerns: you stick to getting the language details right, and let someone else handle the assembly generation! You don’t have to handle the nitty gritty of x86 or ARM or whatever other instruction set, and you don’t have to write common optimizations. Any day you don’t have to unroll loops yourself is a good day.

Okay, so what’s the plan?

We’re going to look at 3 different implementations of gcd. In fact, they’re literally the 3 implementations suggested by wikipedia, transcribed into C code.

We’re going to look at the LLVM IR code emitted by Clang, a C compiler. Then we’re going to run this IR through the LLVM optimizer- and it’s going to try about 100 different optimization passes! - and see how they compare.

If you want to follow along I’ve put all the code in this repo, but you also need to grab an precompiled LLVM binary. More instructions below! You could even grab this code as a starting point to look at how LLVM optimizes your own code! But only if reading assembly is your idea of fun ;)

Okay, onwards!

Following Along

1) Grab the repo:

git clone https://github.com/anniecherk/code_for_website

This repo just has the 3 euclidean algorithm implementations from wikipedia, and all the generated IR.

2) Grab a precompiled LLVM binary (I used 3.9.0), and untar it

3) Add the LLVM binaries to your path:

export LLVM=<wherever you unpacked the llvm files>/clang+llvm-3.9.0-x86_64-apple-darwin/bin/

** or whatever the file is called on your OS, and then add it to your path:

export PATH=$LLVM:$PATH

4) Get the naiive IR by running:

clang -S -emit-llvm gcd1.c

This saves it to a file called <filename>.ll

5) Get the fancy optimized IR by running:

opt -O2 -print-after-all gcd1.ll 2> opt_gcd1.ll

(We use 2> because -print-after-all helpfully prints details of all the passes to stderr, so that’s what we’re redirecting to file). You can also pick and choose which optimizations you want instead of running the prepackaged O2 bundle.

Okay, what we looking at?

We’ve got our 3 gcd functions:

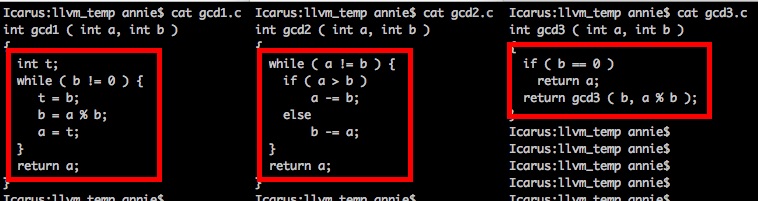
What you might want to know when LLVM assembly

We’re going to look at the LLVM IR in just a hot sec, but first here are some things that might be helpful to know:

i32 is a 32 bit integer, i1 is a 1 bit boolean. Remember this is just the LLVM IR- what this gets physically mapped to depends on your hardware, and decisions that the backends make!

alloca allocates space on the stack that gets released when the function returns.

srem is the signed remainder instruction.

sub nsw is subtraction with No Signed Wrap. This means that if the subtraction underflows the value is poisoned! (How dramatic!)

Here’s the LLVM IR that Clang compiles them to. Ready for a screenful of assembly code? Don’t worry, we’ll talk about it after!

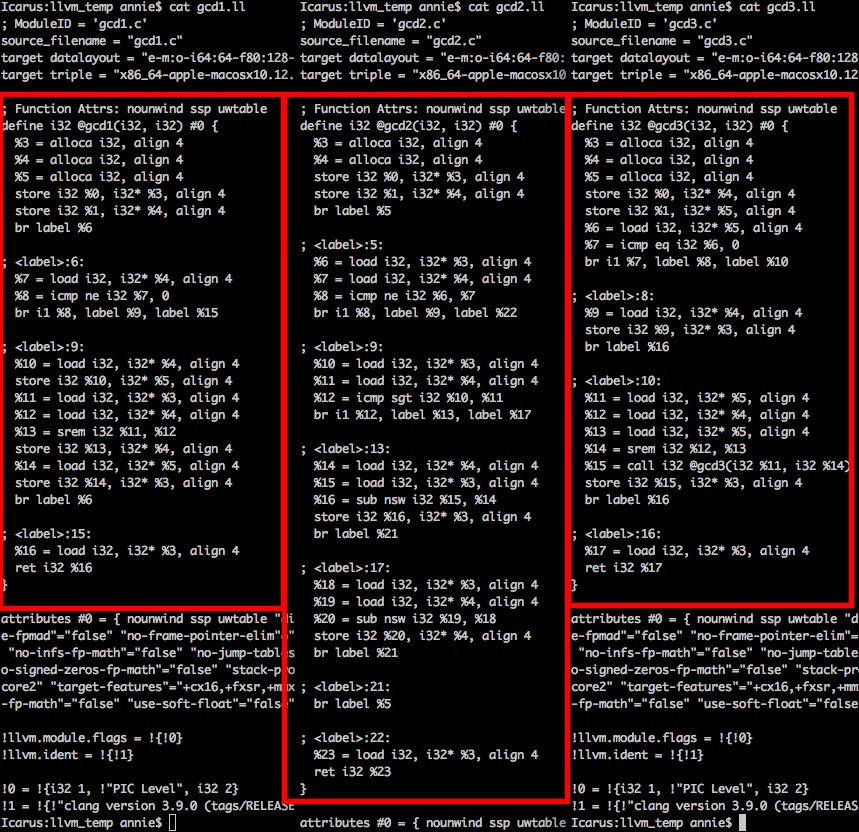
Here’s some interesting things to notice about the above code!

%%%%%% update (01/2019) %%%%%%

When I published this blogpost (11/2016) I wrote that IR generated for gcd1 & gcd3 was the same– it’s definitely not. It’s similar, because the algorithms are similar, but not the same. gcd1 loops: br label %6 / br i1 %8, label %9..., gcd2 has a recursive function call: call i32 @gcd3(.... Thanks to Billy Tetrud for pointing out my mistake.

%%%%%%%%%%%%%%%%%%%%%%%

SSA and The Disposable Variable

Okay, so see all the %1 = ..., %2 = .., %3 = ..., etc assignments? Recall that SSA is Static Single Assignment- this is the single assignment part! In the LLVM IR we have an infinite number of registers, so we never need to reuse them. This makes lots of analyses much easier because you don’t have to worry about when which registers change! The backends handle mapping to physical registers so.. its someone else’s problem :)

Notice that the labels also have unique numbers- and even though the IR for gcd1 and gcd3 is identical the numbers on the labels are slightly different! (ie, ; <label>:9: vs ; <label>:10:)My guess is that Clang first generated label numbers, and then optimized away one of the blocks in gcd3.

SSA and The Basic Block

Now look at how the IR is organized- we’ve got a bunch of blocks of code that start with ; <label>:6: and end with br label %somenumber. Each of these is a basic block. Basic blocks have two rules- there’s only one way in (first line of the block), and one way out (last line of the block- though the way out can be conditional, like a branch!) This control flow does NOT fall through- we always explicitly say where we jump to when we’re done with a given block.

SSA and Phi Nodes

The IR that Clang emitted doesn’t have phi nodes… but we’ll see them in the IR emitted by LLVM so let’s just chat about them now. Phi nodes are how we deal with control flow in SSA. Consider a simple if statement:

if (some_condition):
    y = 2;
else:
    y = 4;
some_function_call( y );

When we get to the code at the bottom of the if statement, we need to know which value of y we need to use, and we signify that the control flow merges back together with a phi node. The phi node goes at the top of the basic block, and selects the correct value for y.

Okay finally! The optimizations!

%% Update (01/19): Again, gcd1 and gcd3 don’t produce the same IR, but here we’ll just look at the optimizations LLVM applies to gcd1 & gcd2 because when I wrote this I thought they did. %%

We’re going to look at side-by-side diffs of the IR for the two functions. I’m just warning you because you’re about to get screenfuls of assembly again. Ready?

Hold your nose cause here goes the cold water…

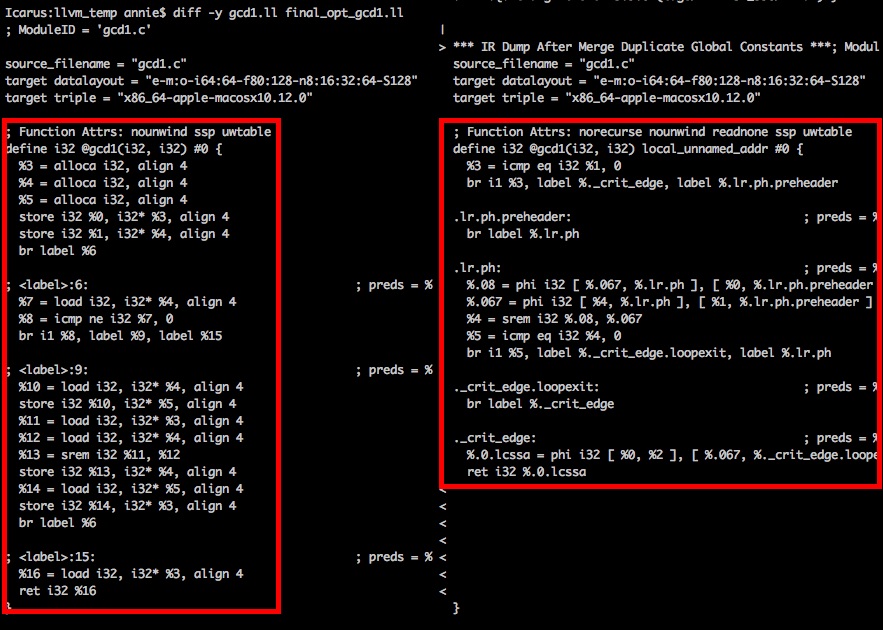
First up! gcd1!

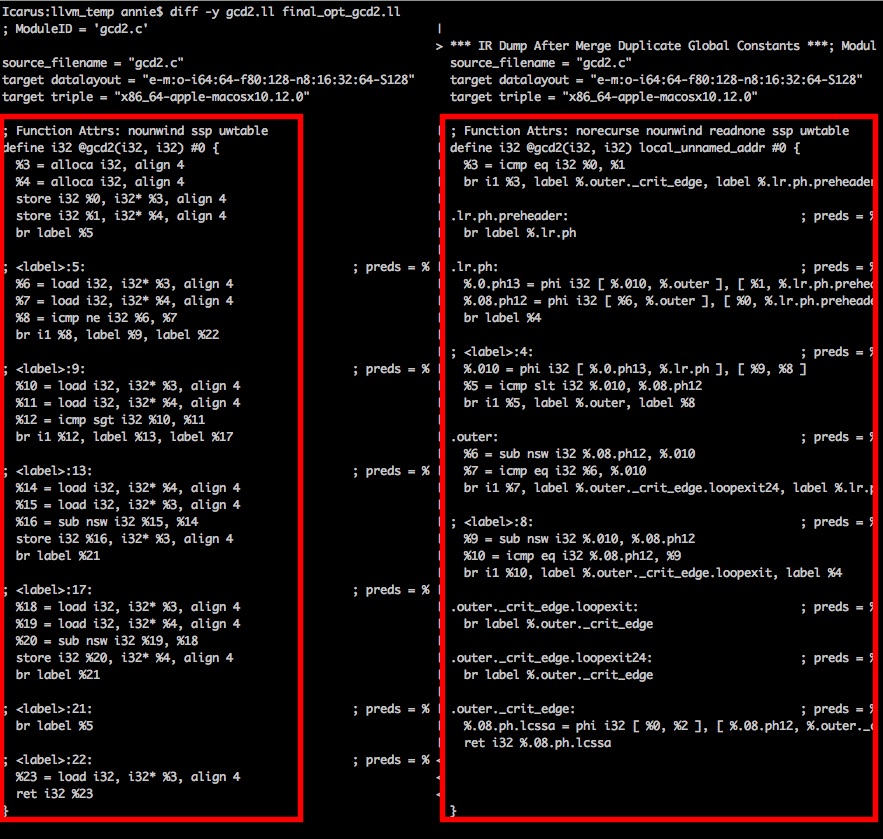
And here’s gd2!

Things to notice

There are those phi nodes we talked about! We also got rid of all the alloca’s, and our labels got split into a preheader, outer, and two outer critcal edge loop exits.

Let’s talk Passes

Okay, so here’s how LLVM optimizations work. When we run the O2 optimization level, this represents a bunch of small optimization passes. (Or, we can select which specific optimizations we want via commandline flags.) An optimization pass either changes something about the IR, or maybe it just collects and annotates information for other passes to use. This means that order matters! Some passes are run lots of times! You can see all the passes LLVM can do and you can even write your own!

There’s way more cool stuff to say about LLVM’s passes than I want to spend time on here, but here is a really great slidedeck.

Which passes optimized our code?

Glad you asked!

SROA: Scalar Replacement of Aggregates

The very first thing that ran was SROA, the goal of which is to get rid of alloca’s. All the alloca’s got replaced with phi nodes! That’s where they all came from…

Loop-Closed SSA Form

Added an extra phi node- this is one of the annotation passes, it adds phi nodes for every ‘live’ variable at the end of the basic block because this might expose optimizations done by other passes.

Rotate Loops

This is what architecture calls ‘software pipelining’. If your loop does thingA and then thingB, you can move thingA out above the loop, then ‘rotate’ the loop so it looks like thingB and then thingA.. and then do some cleanup. I assume this is also done in search of more optimizations.

Simplify the CFG (Control Flow Graph)

In general, simplyifycfg is responsible for gutting dead code, and combining basic blocks that can combined. This pass introduced the ._crit_edge: label.

Canonicalize Natural Loops

This pass introduced the preheader and loopexit labels. In general, this pass turns loops into a more structured canonical form which exposes them to other optimizations. This fits consistently with LLVM’s pass strategy: canonicalize, simplify, lower.

Global Variable Numbering

This pass got rid of one of the phi nodes that closed loop SSA form introduced. At least we’re netting zero?